Class 9th B and 9th C
Wednesday, January 14, 2026
Free ppt for editing for Class 9th
Download these ppt in your system and do experiment in powerpoint software.
Sunday, July 25, 2021
Mathematics test class 10th │ Maths test │ Coordinate Geometry test
Class 10 Maths MCQs Chapter 7 Coordinate Geometry
1. The distance of the point P(2, 3) from the x-axis is
(a) 2
(b) 3
(c) 1
(d) 5
Answer/ Explanation
Answer: b
Explaination: Reason: The distance from x-axis is equal to its ordinate i.e., 3
2. The distance between the point P(1, 4) and Q(4, 0) is
(a) 4
(b) 5
(c) 6
(d) 3√3
Answer/ Explanation
Answer: b
Explaination: Reason: The required distance = \(\sqrt{(4-1)^{2}+(0-4)^{2}}=\sqrt{9+16}=\sqrt{25}=5\)
3. The points (-5, 1), (1, p) and (4, -2) are collinear if
the value of p is
(a) 3
(b) 2
(c) 1
(d) -1
Answer/ Explanation
Answer: d
Explaination: Reason: The points are collinear if area of Δ = 0
= \(\frac{1}{2}\)[-5(p + 2) +l(-2 -1) + 4(1 – p)] – 0
⇒ -5 p -10-3 + 4-4p = 0
⇒ -9p = +9
∴ p = -1
4. The area of the triangle ABC with the vertices A(-5, 7), B(-4, -5) and C(4, 5) is
(a) 63
(b) 35
(c) 53
(d) 36
Answer/ Explanation
Answer: c
Explaination: Reason: Area of ΔABC = \(\frac{1}{2}\) [x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= \(\frac{1}{2}\)[-5(-5 – 5) -4(5 – 7) + 4(7 – (-5))] = \(\frac{1}{2}\)[-5(-10) -4(-2) + 4(12)]
= \(\frac{1}{2}\)[50 + 8 + 48] = \(\frac{1}{2}\) × 106 = 53 sq. units
5. The distance of the point (α, β) from the origin is
(a) α + β
(b) α² + β²
(c) |α| + |β|
(d) \(\sqrt{\alpha^{2}+\beta^{2}}\)
Answer/ Explanation
Answer: d
Explaination: Reason: Distance of (α, β) from origin (0, 0) = \(\sqrt{(\alpha-0)^{2}+(\beta-0)^{2}}=\sqrt{\alpha^{2}+\beta^{2}}\)
6. The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is
(a) 11
(b) 22
(c) 33
(d) 21
Answer/ Explanation
Answer: a
Explaination: Reason: Required area= \(\frac{1}{2}\)[1(3 + 4) -2(-4 – 2) -3(2 – 3)]
= \(\frac{1}{2}\)[7 + 12 + 3]
= \(\frac{1}{2}\) × 22 = 11
7. The line segment joining the points (3, -1) and (-6, 5) is trisected. The coordinates of point of trisection are
(a) (3, 3)
(b) (- 3, 3)
(c) (3, – 3)
(d) (-3,-3)
Answer/ Explanation
Answer: b
Explaination: Reason: Since the line segment AB is trisected
8. The line 3x + y – 9 = 0 divides the line joining the points (1, 3) and (2, 7) internally in the ratio
(a) 3 : 4
(b) 3 : 2
(c) 2 : 3
(d) 4 : 3
Answer/ Explanation
Answer: a
Explaination: Reason: Let the line 3x + y – 9 = 0 divide the line segment joining A(l, 3) ad B(2, 7) in the ratio K : 1 at point C.
9. The distance between A (a + b, a – b) and B(a – b, -a – b) is
Answer/ Explanation
Answer: c
Explaination:
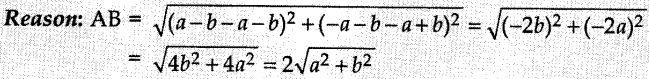
10. If (a/3, 4) is the mid-point of the segment joining the points P(-6, 5) and R(-2, 3), then the value of ‘a’ is
(a) 12
(b) -6
(c) -12
(d) -4
Answer/ Explanation
Answer: c
Explaination:
11. If the distance between the points (x, -1) and (3, 2) is 5, then the value of x is
(a) -7 or -1
(b) -7 or 1
(c) 7 or 1
(d) 7 or -1
Answer/ Explanation
Answer: d
Explaination: Reason: We have \(\sqrt{(x-3)^{2}+(-1-2)^{2}}=5\)
⇒ (x – 3)² + 9 = 25
⇒ x² – 6x + 9 + 9 = 25
⇒ x² -6x – 7 = 0
⇒ (x – 7)(x + 1) = 0
⇒ x = 7 or x = -1
12. The points (1,1), (-2, 7) and (3, -3) are
(a) vertices of an equilateral triangle
(b) collinear
(c) vertices of an isosceles triangle
(d) none of these
Answer/ Explanation
Answer: b
Explaination: Reason: Let A(1, 1), B(-2, 7) and C(3, 3) are the given points, Then, we have
13. The coordinates of the centroid of a triangle whose vertices are (0, 6), (8,12) and (8, 0) is
(a) (4, 6)
(b) (16, 6)
(c) (8, 6)
(d) (16/3, 6)
Answer/ Explanation
Answer: d
Explaination: Reason: The co-ordinates of the centroid of the triangle is
14. Two vertices of a triangle are (3, – 5) and (- 7,4). If its centroid is (2, -1), then the third vertex is
(a) (10, 2)
(b) (-10,2)
(c) (10,-2)
(d) (-10,-2)
Answer/ Explanation
Answer: c
Explaination: Reason: Let the coordinates of the third vertex be (x, y)
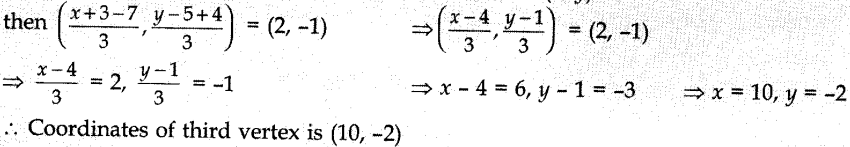
15. The area of the triangle formed by the points A(-1.5, 3), B(6, -2) and C(-3, 4) is
(a) 0
(b) 1
(c) 2
(d) 3/2
Answer/ Explanation
Answer: a
Explaination: Reason: Area of ΔABC = \(\frac{1}{2}\) [-1.5(-2 – 4) + 6(4 – 3) + (-3) (3 + 2)] = \(\frac{1}{2}\) [9 + 6 – 15] = 0. It is a straight line.
16. If the points P(1, 2), B(0, 0) and C(a, b) are collinear, then
(a) 2a = b
(b) a = -b
(c) a = 2b
(d) a = b
Answer/ Explanation
Answer: a
Explaination: Reason: Area of ΔPBC = 0
⇒ \(\frac{1}{2}\)[1(0 – b) + 0(6 – 1) + a(2 – 0)] = 0
⇒ \(\frac{1}{2}\)[-6 + 2a] = 0
⇒ -b + 2a = 0
∴ 2a = b
Mathematics test class 10th │ Maths test │Coordinate Geometry Test
Mathematics test class 10th │ Maths test │ Free maths test │ Class 10th Maths test
To give test, Click on:
Mathematics Test
Hello everyone. This is Mohit Sharma. I want to inform you that this is a practice test paper of Mathematics. First read all the guidelines then after that you can attempt this short quiz. Here a link is given to you at last. Click on the link and attempt this short quiz.
सभी को नमस्कार। मेरा नाम मोहित शर्मा है । मैं आपको सूचित करना चाहता हूं कि यह Maths का एक अभ्यास परीक्षण पेपर है। सभी दिशानिर्देशों को पढ़ें इसके बाद आप इस संक्षिप्त प्रश्नोत्तरी का प्रयास कर सकते हैं।
यहां पर आपको आखिरी में एक लिंक दिया गया है। लिंक पर क्लिक करें और इस संक्षिप्त प्रश्नोत्तरी का प्रयास करें।
ALL THE BEST. ✌
Guidelines:
Total Questions: 10
Max. marks: 10 (Each question carry 1 mark)
Subject: Mathematics
Topic: Coordinate Geometry
After attempting short quiz you will get your SCORE on screen with correct answers if you have done any question incorrect.
Tuesday, July 13, 2021
Mathematics test class 10th │ Maths test │ Free maths test │ Class 10th Maths test
Mathematics test class 10th │ Maths test │ Free maths test │ Class 10th Maths test
To give test, Click on:
Mathematics Test
Hello everyone. This is Mohit Sharma. I want to inform you that this is a practice test paper of Mathematics. First read all the guidelines then after that you can attempt this short quiz. Here a link is given to you at last. Click on the link and attempt this short quiz.
सभी को नमस्कार। मेरा नाम मोहित शर्मा है । मैं आपको सूचित करना चाहता हूं कि यह Maths का एक अभ्यास परीक्षण पेपर है। सभी दिशानिर्देशों को पढ़ें इसके बाद आप इस संक्षिप्त प्रश्नोत्तरी का प्रयास कर सकते हैं। यहां पर आपको आखिरी में एक लिंक दिया गया है। लिंक पर क्लिक करें और इस संक्षिप्त प्रश्नोत्तरी का प्रयास करें।
ALL THE BEST. ✌
Guidelines:
Total Questions: 5
Max. marks: 10 (Each question carry 2 mark)
Subject: Computer
School: J.P. PUBLIC ACADEMY, KASGANJ
After attempting short quiz you will get your SCORE on screen with correct answers if you have done any question incorrect.
Computer test class 7th │ Computer test │ Free computer test │ Class 7th Computer test
Computer test class 7th │ Computer test │ Free computer test │ Class 7th Computer test
To give test, Click on:
Computer Test
Hello everyone. This is Mohit Sharma. I want to inform you that this is a practice test paper of Computer. First read all the guidelines then after that you can attempt this short quiz. Here a link is given to you at last. Click on the link and attempt this short quiz.
सभी को नमस्कार। मेरा नाम मोहित शर्मा है । मैं आपको सूचित करना चाहता हूं कि यह COMPUTER का एक अभ्यास परीक्षण पेपर है। सभी दिशानिर्देशों को पढ़ें इसके बाद आप इस संक्षिप्त प्रश्नोत्तरी का प्रयास कर सकते हैं। यहां पर आपको आखिरी में एक लिंक दिया गया है। लिंक पर क्लिक करें और इस संक्षिप्त प्रश्नोत्तरी का प्रयास करें।
ALL THE BEST. ✌
Guidelines:
Total Questions: 10
Max. marks: 10 (Each question carry 1 mark)
Subject: Computer
School: J.P. PUBLIC ACADEMY, KASGANJ
After attempting short quiz you will get your SCORE on screen with correct answers if you have done any question incorrect.
Featured Post
[BEST] Free download RS Aggarwal solutions in pdf
[BEST] Free download RS Aggarwal solutions in pdf Download Free pdf solutions of RS Aggarwal RS Aggarwal is an unmissable...
Most Popular Posts
-
आयु सम्बन्धी प्रश्न और हल – Age Related Question of Maths in Hindiआयु सम्बन्धी प्रश्न और हल – Age Related Question of Maths in Hindi ... -
Ncert solutions of class 10 | Free download ncert solutions NCERT ...
