Trigonometry | Trigonometry hand trick | Trigonometry Class 10 | Trigonometry tricks | त्रिकोणमिति

Trigonometry | Trigonometry hand trick | Trigonometry Class 10 | Trigonometry tricks | त्रिकोणमिति

 Quadratic Formula | द्विघात समीकरण | Quadratic Equation Tricks | How To Solve Quadratic Equations

Video on Youtube:

Trigonometry | Trigonometry hand trick | Trigonometry Class 10 | Trigonometry tricks  | त्रिकोणमिति

Trigonometry | Trigonometry hand trick | Trigonometry Class 10 | Trigonometry tricks | त्रिकोणमिति

Trigonometry | Trigonometry hand trick | Trigonometry Class 10 | Trigonometry tricks | त्रिकोणमिति About this video: Solve Trigonometry questions in 3 seconds. Trigonometry shortcut for JEE/NDA/NA/AIRFORCE/RAILWAYS/ BANKING/SSC-CGL/MBA/GRE/SAT/CETs./Competitive exams. Hey guys This is Mohit Sharma. Welcome to our youtube channel Style stardum MS. SUBSCRIBE( it's free): Style stardum MS- https://www.youtube.com/channel/UCMzOdlcCIVacd9Bw7CM5Pnw?view_as=subscriber maths study- https://www.youtube.com/channel/UCQNspKbWcNnibwaIH1vY_yA?view_as=subscriber ___________________________________________________________________________________ Our apps: maths study: https://play.google.com/store/apps/details?id=com.app.mathematicsnew maths study 2: https://play.google.com/store/apps/details?id=in.co.mathsstudy.ms __________________________________________________________________________________ Our Social links- ●Youtube- https://www.youtube.com/channel/UCMzOdlcCIVacd9Bw7CM5Pnw?view_as=subscriber ●Facebook- https://www.facebook.com/mohitsharma.ksj ●Twitter- https://www.twitter.com/MohitKsj ●Instagram- https://www.instagram.com/mohitsharma_163/ ●Website- https://www.mathsstudy.co.in ● Other youtube official channel of maths- https://www.youtube.com/channel/UCQNspKbWcNnibwaIH1vY_yA ●Pinterest- https://pin.it/66WthEK ●Quora - Come and Join.... https://www.quora.com/q/zjrbytriwtrjpsjt?invite_code=u75iHFSa8qMSb74a5w5s Email- mohitsharma.ksj@gmail.com ___________________________________________________________________________________  @Style stardum MS   @Dear Sir   @SSC MAKER  @Unacademy UPSC Hindi   @wifistudy   @Vedantu Class 9 & 10   @BYJU'S   @Magnet Brains  Trigonometry,Trigonometry hand trick ,Trigonometry Class 10/11/12,Trigonometry tricks in hindi,Style stardum MS,trigonometry class 10th in hindi,class 10 chapter 8,trigonometry,trigonometry formulas,trigonometry trick,trigonometry class 10,trigonometry class 11,trigonometry class 12,trigonometry table,trigonometry ratios,trigonometry tricks,trigonometry basics,math shortcut and tricks,ssc-cgl math tricks,jee tricks maths, #TRIGONMETRYTRICKS #TRIGONOMETRYTRICKS #math #mathematics #maths #NEHAMATHTRICKS ___________________________________________________________________________________ trigonometry tricks,trigonometry shortcuts,math shortcut and tricks,trigonometry cbse isc class xii 12th,trigonometry cbse isc class xi 11th,mathematically inclined,neha agarwal maths,jee tricks math,nda/na math tricks,eamcet/gujcet/mhcet/kcet/comedk math tricks,sat / gre/mba tricks,banking/railways/airforce math tricks,ssc-cgl math tricks,trigonometry,trigonometry basics,trigonometry tricks,basic trigonometry,pythagorean theorem,trigonometry trick,trigonometry table,sin cos tan - basic trigonometry in hindi,trigonometry ssc cgl,trigonometry concept,trigonometry introduction,math,maths,mathematics,trigonometry class 10 chapter 8,trigonometry tricks,class 10 maths,maths class 10,trigonometry table,right triangle trigonometry, trigonometry class 11,trigo class 11,class 11 maths chapter 3,trigonometric functions class 11,radian to degree,trigonometry class 11 important questions,trigonometry shortcut tricks,trigonometry tricks class 11,trigonometry basics,trigonometric functions,trigonometry,trigonometry formulas,trigonometry trick,trigonometry table,trigonometry ratios,trigonometry functions,chapter 3 trigo class 11,chapter 3 trigonometry class 11,trigonometry ssc cgl, _______________________________________________________________________________________ Trigonometry Class 10 Maths | Trigonometry Formulas/Table Tricks | Trigonometry Questions Tricks Solve Trigonometry in 10 Seconds | IIT JEE Short Cuts & Tricks | JEE Main 2021 | Score Quick Marks Math Shortcuts for JEE Mains | Advanced | BITSAT | VITEEE | WBJEE. Learn the super awesome Tricks that will blow your mind. jee mains maths | jee main mock test | jee mains 2021 | jee mains mathematics | jee mock test | jee 2021 | jee maths | jee main mock test 2021| iit jee 2021 | iitmaths | jee mains mock test free online | jee exam 2021 | iit jee maths | jee main online mock test | jee mains exam | iit jee maths lectures | jee maths lectures CBSE Class 11 Math Trigonometric Functions | Class 11 NCERT chapter 1 | Domain Range | Sin, Cos, Tan, Cosec, Sec, Cot | Formula Short cut| Memory tip | Trigonometry Short Tricks |Trigonometry Identities | Trigonometry Equation | General and Principal Solution | Important Practice Questions | Angle Radian Degree | Crash Course Class 11 Trigonometric Functions| Sets Complete Chapter in 1 video | Formulas Trick | Trigonometry Class 11 | Trigonometry ssc cgl _______________________________________________________________________________________

Quadratic Formula | द्विघात समीकरण | Quadratic Equation Tricks | How To Solve Quadratic Equations

 Quadratic Formula | द्विघात समीकरण | Quadratic Equation Tricks | How To Solve Quadratic Equations

_________________________________________________

Youtube Video: Quadratic Formula

An example of a Quadratic Equation:

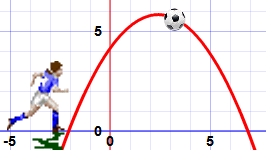
The function makes nice curves like this one:

Name

The name Quadratic comes from "quad" meaning square, because the variable gets  squared (like x²).

It is also called an "Equation of Degree 2" (because of the "2" on the x)

Youtube Video: Quadratic Formula

Standard Form

The Standard Form of a Quadratic Equation looks like this:

• a, b and c are known values. a can't be 0.

• "x" is the variable or unknown (we don't know it yet).

 

Here are some examples:

2x2 + 5x + 3 = 0		In this one a=2, b=5 and c=3
x2 − 3x = 0		This one is a little more tricky: Where is a? Well a=1, as we don't usually write "1x2" b = −3 And where is c? Well c=0, so is not shown.
5x − 3 = 0		Oops! This one is not a quadratic equation: it is missing x2 (in other words a=0, which means it can't be quadratic) Youtube Video: Quadratic Formula Hidden Quadratic Equations! As we saw before, the Standard Form of a Quadratic Equation is ax2 + bx + c = 0 But sometimes a quadratic equation doesn't look like that! For example: In disguise In Standard Form a, b and c x2 = 3x − 1 Move all terms to left hand side x2 − 3x + 1 = 0 a=1, b=−3, c=1 2(w2 − 2w) = 5 Expand (undo the brackets), and move 5 to left 2w2 − 4w − 5 = 0 a=2, b=−4, c=−5 z(z−1) = 3 Expand, and move 3 to left z2 − z − 3 = 0 a=1, b=−1, c=−3

About the Quadratic Formula

Plus/Minus

First of all what is that plus/minus thing that looks like ± ?

The ± means there are TWO answers:

x = −b + √(b² − 4ac)2a

x = −b − √(b² − 4ac)2a

Here is an example with two answers:

But it does not always work out like that!

• Imagine if the curve "just touches" the x-axis.
• Or imagine the curve is so high it doesn't even cross the x-axis!

This is where the "Discriminant" helps us ...

Youtube Video: Quadratic Formula

Discriminant

Do you see b² − 4ac in the formula above? It is called the Discriminant, because it can "discriminate" between the possible types of answer:

• when b² − 4ac is positive, we get two Real solutions
• when it is zero we get just ONE real solution (both answers are the same)
• when it is negative we get a pair of Complex solutions

Complex solutions? Let's talk about them after we see how to use the formula.

Youtube Video: Quadratic Formula

 

Using the Quadratic Formula

Just put the values of a, b and c into the Quadratic Formula, and do the calculations.

Example: Solve 5x² + 6x + 1 = 0

Coefficients are:a = 5, b = 6, c = 1

Quadratic Formula:x = −b ± √(b² − 4ac)2a

Put in a, b and c:x = −6 ± √(6² − 4×5×1)2×5

Solve:x = −6 ± √(36 − 20)10

 x = −6 ± √(16)10

 x = −6 ± 410

 x = −0.2 or −1

 

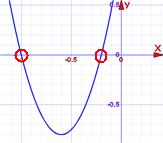
Answer: x = −0.2 or x = −1

 

And we see them on this graph.

Check -0.2:		5×(−0.2)2 + 6×(−0.2) + 1 = 5×(0.04) + 6×(−0.2) + 1 = 0.2 − 1.2 + 1 = 0
Check -1:		5×(−1)2 + 6×(−1) + 1 = 5×(1) + 6×(−1) + 1 = 5 − 6 + 1 = 0

Example: Solve x² − 4x + 6.25 = 0

Coefficients are:a=1, b=−4, c=6.25

Note that the Discriminant is negative:b² − 4ac = (−4)² − 4×1×6.25
              = −9

Use the Quadratic Formula:x = −(−4) ± √(−9)2

√(−9) = 3i
(where i is the imaginary number √−1)

So:x = 4 ± 3i2

 

Answer: x = 2 ± 1.5i

 

The graph does not cross the x-axis. That is why we ended up with complex numbers.

BUT an upside-down mirror image of our equation does cross the x-axis at 2 ± 1.5 (note: missing the i).

Just an interesting fact for you!

____________________________________________________________

Youtube Video: Quadratic Formula

A quadratic equation is a second-order polynomial equation in a single variable 

(1)

with . Because it is a second-order polynomial equation, the fundamental theorem of algebra guarantees that it has two solutions. These solutions may be both real, or both complex.

Among his many other talents, Major General Stanley in Gilbert and Sullivan's operetta the Pirates of Penzance impresses the pirates with his knowledge of quadratic equations in "The Major General's Song" as follows: "I am the very model of a modern Major-General, I've information vegetable, animal, and mineral, I know the kings of England, and I quote the fights historical, From Marathon to Waterloo, in order categorical; I'm very well acquainted too with matters mathematical, I understand equations, both the simple and quadratical, About binomial theorem I'm teeming with a lot o' news-- With many cheerful facts about the square of the hypotenuse."

The roots  can be found by completing the square,

(2)

src="https://mathworld.wolfram.com/images/equations/QuadraticEquation/NumberedEquation3.gif" style="border: 0px;" width="217" />

(3)

(4)

Solving for  then gives

(5)

This equation is known as the quadratic formula.

Here are the steps required to solve a quadratic using the quadratic formula:

Youtube Video: Quadratic Formula

Adding Polynomials | Polynomials Class 10/9 | Class 10 Maths Chapter 2 | Basics of Polynomial

Adding Polynomials | Polynomials Class 10/9 | Class 10 Maths Chapter 2 | Basics of Polynomial

 

Polynomial addition and subtraction

Youtube video:-

Adding Polynomials | Polynomials Class 10/9 | Class 10 Maths Chapter 2 | Basics of Polynomial

Our apps in Play store:

maths study
maths study 2

__________________________________________________________________________________

SUBSCRIBE( it's free): Style stardum MS- https://www.youtube.com/channel/UCMzO... maths study- https://www.youtube.com/channel/UCQNs... ___________________________________________________________________________________ Our Social links- ●Youtube- https://www.youtube.com/channel/UCMzO... ●Facebook- https://www.facebook.com/mohitsharma.ksj ●Twitter- https://www.twitter.com/MohitKsj ●Instagram- https://www.instagram.com/mohitsharma... ●Website- https://www.mathsstudy.co.in ● Other youtube official channel of maths- https://www.youtube.com/channel/UCQNs... ●Pinterest- https://pin.it/66WthEK ●Quora - Come and Join.... https://www.quora.com/q/zjrbytriwtrjp...

_____________________________________________________________________________

Adding Polynomials | Polynomials Class 10/9 | Class 10 Maths Chapter 2 | Basics of Polynomial math,maths,mathematics,polynomials,cbse,class 10,class 10 maths,polynomials class 10,polynomials class 9,class 10 maths chapter 2,class 10 maths chapter,polynomial class 9,polynomial long division,polynomial,polynomial regression,polynomial functions,polynomial equations,polynomial division,minimal polynomial,chromatic polynomial,graph theory,polynomials class 10 cbse,long division,polynomial long division,class 10 polynomials,long division of polynomials,Style stardum MS polynomials full chapter (part 1) class 10,cbse class 10 maths chapter 2,polynomials class 10 cbse,class 10 maths,class 10 maths chapter 2,polynomials class 10 ncert,polynomials class 10,ncert maths class 10,maths class 10 chapter 2,magnet brains,10th maths chapter polynomials,10th maths rs aggarwal,maths class 10 chapter polynomials,class 10 chapter 2 polynomials,10th maths what are polynomials,class 10 maths polynomials introduction,class 10th maths polynomial adding polynomials,Style stardum MS,how to add polynomials,what are like terms?,add like terms,polynomial class 10,polynomial class 9,addition and subtraction,subtract polynomial,column method,additioon and subtraction of polynomials,J.P. PUBLIC ACADEMY,kasganj maths,class 10th chapter 2,chapter 2 polynomial,maths study,math,algebra,polynomials class 10 ncert,class 10 maths chapter 2,polynomials class 10,mathematics,mathematics class 8th,bsda ksj #polynomial #ncert #mathematics #class10th

Algebraic Expression│Class 7 RS Aggarwal │Introduction of chapter 6

Algebraic Expression│Class 7 RS Aggarwal │Introduction of chapter 6

 

Algebraic Expression│Class 7 RS Aggarwal │Introduction of chapter 6│Class 7 chapter 6 in hindi

Youtube Video:- Algebraic Expressions

What is an Algebraic Expression?

An algebraic expression in mathematics is an expression which is made up of variables and constants, along with algebraic operations (addition, subtraction, etc.). Expressions are made up of terms.  They are also termed algebraic equations. 

Examples

3x + 4y – 7,  4x – 10, etc.

These expressions are represented with the help of unknown variables, constants and coefficients. The combination of these three (as terms) is said to be an expression. It is to be noted that, unlike the algebraic equation, an algebraic expression has no sides or equal to sign. Some of its examples include

• 3x + 2y – 5
• x – 20
• 2x2 − 3xy + 5

Variables, Coefficient & Constant

In Algebra we work with Variable, Symbols or Letters whose value is unknown to us.

In the above expression (i.e. 5x – 3),

• x is a variable, whose value is unknown to us which can take any value.
• 5 is known as the coefficient of x, as it is a constant value used with the variable term and is well defined.
• 3 is the constant value term which has a definite value.

The whole expression is known to be the Binomial term, as it has two unlikely terms.

Types of Algebraic expression

There are 3 main types of algebraic expressions which include:

• Monomial Expression
• Binomial Expression
• Polynomial Expression

Monomial Expression

An algebraic expression which is having only one term is known as a monomial.

Examples of monomial expression include 3x4, 3xy, 3x, 8y, etc.

Binomial Expression

A binomial expression is an algebraic expression which is having two terms, which are unlike.

Examples of binomial include 5xy + 8, xyz + x3, etc.

Polynomial Expression

In general, an expression with more than one terms with non-negative integral exponents of a variable is known as a polynomial.

Examples of polynomial expression include ax + by + ca,  x3 + 2x + 3, etc.

Other Types of Expression:

Apart from monomial, binomial and polynomial types of expressions, an algebraic expression can also be classified into two additional types which are:

• Numeric Expression
• Variable Expression

Numeric Expression

A numeric expression consists of numbers and operations, but never include any variable. Some of the examples of numeric expressions are 10 + 5, 15 ÷ 2, etc.

Variable Expression

A variable expression is an expression which contains variables along with numbers and operation to define an expression. A few examples of a variable expression include 4x + y, 5ab + 33, etc.

Algebraic expression for Class 7

In Class 7, students will come across the terms of algebraic equations such as:

• Coefficient of a term
• Variables
• Constant 
• Factors of a term
• Terms of equations
• Like and Unlike terms

Example of using these terms are given below.

If 2x2+3xy+4x+7 is an algebraic expression.

Then, 2x2, 3xy, 4x and 7 are the terms

Coefficient of term x2 = 2

Constant term = 7

Example of like and unlike terms: 

Like terms: 2x and 3x 

Unlike terms: 2x and 3y

Factors of a term:

If 3xy is a term, then its factors are 3, x and y.

Monomial, Binomial & Trinomial

Also, in grade 7 we will learn about types of expressions, such as monomial, binomial and trinomial. Let us see examples of each.

Monomial: 2x

Binomial: 2x+3y

Trinomial: 2x+3y+9

Addition and Subtraction of Algebraic Expressions

We can add and subtract like terms easily. 

Example: Add 3x + 5y – 6z and x – 4y + 2z.

By adding both the expressions we get;

(3x + 5y – 6z) + (x – 4y + 2z)

Separating the like terms and adding them together:

(3x + x) + (5y – 4y) + (-6z + 2z)

4x + y – 4z

Formulas

The general algebraic formulas we use to solve the expressions or equations are:

• (a + b)2 = a2 + 2ab + b2
• (a – b)2 = a2 – 2ab + b2
• a2 – b2 = (a – b)(a + b)
• (a + b)3 = a3 + b3 + 3ab(a + b)
• (a – b)3 = a3 – b3 – 3ab(a – b) 
• a3 – b3 = (a – b)(a2 + ab + b2)
• a3 + b3 = (a + b)(a2 – ab + b2)

Solved Problem

Example: Simplify the given expressions by combining the like terms and write the type of Algebraic expression. (i) 3xy­­3 + 9x2 y3 + 5y3x (ii) 7ab2 c2 + 2a3 b2 − 3abc – 5ab2 c2 – 2b2 a3 + 2ab (iii) 50x3 – 20x + 8x + 21x3 – 3x + 15x – 41x3 Solution: Creating a table to find the solution: S.no Term Simplification Type of Expression 1 3xy­­3 + 9x2 y3 + 5y3x 8xy3 + 9x2y3 Binomial 2 7ab2 c2 + 2a3 b2 − 3abc – 5ab2 c2 – 2b2 a3 + 2ab 2ab2 c2 − 3abc + 2ab Trinomial 3 50x3 – 20x + 8x + 21x3 – 3x + 15x – 41x3 30x³ Monomial

____________________________________________________________________

Algebraic Expression│Class 7 RS Aggarwal │Introduction of chapter 6│Class 7 chapter 6 in hindi Hey guys This is Mohit Sharma. Welcome to our youtube channel Style stardum MS. SUBSCRIBE( it's free): Style stardum MS- https://www.youtube.com/channel/UCMzO... maths study- https://www.youtube.com/channel/UCQNs... ___________________________________________________________________________________ Our Social links- ●Youtube- https://www.youtube.com/channel/UCMzO... ●Facebook- https://www.facebook.com/mohitsharma.ksj ●Twitter- https://www.twitter.com/MohitKsj ●Instagram- https://www.instagram.com/mohitsharma... ●Website- https://www.mathsstudy.co.in ● Other youtube official channel of maths- https://www.youtube.com/channel/UCQNs... ●Pinterest- https://pin.it/66WthEK ●Quora - Come and Join.... https://www.quora.com/q/zjrbytriwtrjp... ___________________________________________________________________________________ Algebraic Expressions,Class 7 Examples, complete rules,RS Aggarwal Chapter 6,Algebra in hindi,addition trick,subtraction trick,Style stardum MS,bsda ksj,rs aggarwal solutions,rs aggarwal class 7,rs aggarwal chapter 6,rs aggarwal answers in hindi,algebraic expressions in hindi,sjs public school,J.P. PUBLIC ACADEMY,maths rs aggarwal class 7,algebraic expressions class 8,simplifying algebraic expressions,algebra,learn maths,algebraic expression introduction,basics of chapter 6, #rsaggarwal #maths #algebra #chapter6 #class7 #mathematics #learnmaths

_________________________________________________________________________